Las matemáticas para siempre

Eduardo Sáenz de Cabezón une la ciencia con el humor y los relatos. Es Licenciado en Teología y Doctor en Matemáticas, es autor de varias charlas divulgativas sobre su área que imparte en universidades y centros de educación secundaria. Es narrador oral para niños, jóvenes y adultos. Ejerce como Profesor de las asignaturas Informática, Sistemas Informáticos, Matemática Discreta y Álgebra, en la Universidad de La Rioja, desde 2010. También es tutor de Trabajos de Grado y Maestría en las titulaciones de Informática y Matemáticas. Publicó artículos de investigación y es autor del show matemático “El baúl de Pitágoras”, que fue exhibido en teatros y bares en varias ciudades de España desde 2012. Ganó el concurso de monólogos científicos FameLab en España, 2013. Es uno de los fundadores del grupo de monologuistas científicos “The Big Van Theory” con más de 200 representaciones en España entre 2013 y 2014. Nació en Logroño, España, en 1972. Recibido en la Universidad Pontificia de Comillas, en 1996, además obtuvo su Licenciatura y Doctorado en Matemáticas en la Universidad de La Rioja.

Conjetura de Collatz

El teorema de Collatz dice que si coges cualquier numero natural par, se divide entre dos y si es impar se multiplica por tres y se suma uno.Al final seguirás haciendo esto hasta llegar a 1,si sigues se irán repitiendo los números.
Por ejemplo;
6:3,10,5,16,8,4,2,1
25:76,38,19,58,29,88,44,22,11,34,17,51,153,460,230,115,346,173,520,260,130,65,196,98,49,148,74,37,112,56,28,14,7,22,11,34,17,52,26,13,40,20,10,5,15,46,23,70.35,106,53,160,80,40,20,10,5,16,8,4,2,12

Top 10 mejores científicos

Isaac Newton

Marie Curie

Stephen Hawking

Albert Einstein

Nikola Tesla

¿Cómo dividir un segmento en partes iguales?

Números decimales en la recta numérica

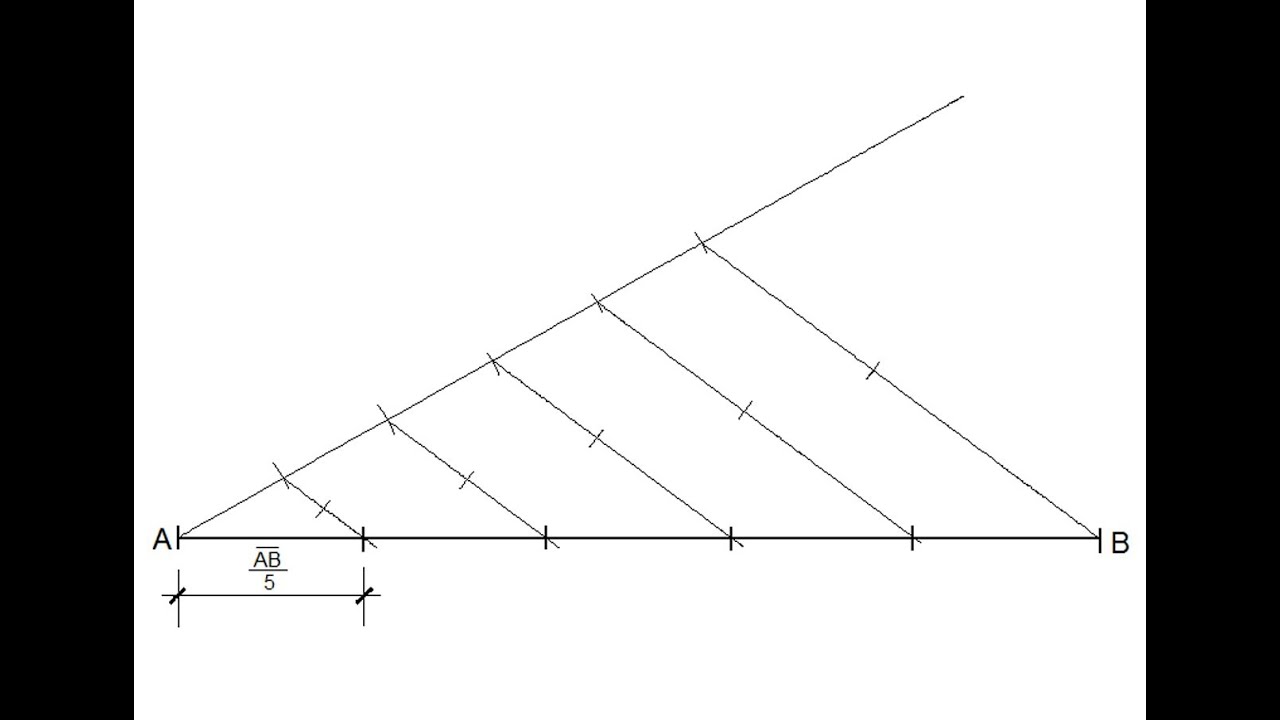
Dividir un segmento en partes iguales

Para dividir un segmento en dos partes iguales basta con utilizar la mediatriz. Pero si queremos dividir el segmento en 3, 5, 6 o más partes iguales, la mediatriz no nos sirve y habrá que utilizar el procedimiento que se explica a continuación.
Esta operación es muy importante ya que permite poder dividir un segmento en un número de partes que se desee. Vamos a ver, como ejemplo, la división del segmento AB en 5 partes iguales.

Ejecicios resueltos

a) 3 · (2 − 7) − 5 · (3 − 6) + 2 · ( 8 − 15 ) + 4 · (11 − 9) = -6

b) (4 − 6) · (8 − 3) − (5 − 9) · (1 − 7) + 18 = -16

c) 3 · (5 − 9 + 2) − 8 · (3 − 6 − 2) + 4 · (5 − 12) = 6

d) 20 − 2 · [10 − 3 · (6 − 9)] = -18

e) 18 + 3 · (8 − 12) − 4 · [5 − 3 · (6 + 3 − 5 · 2 )] = -26

f) 21 − 8 · (10 − 4) + (8 − 11) · [5 + (3 − 6) · (8 − 2)] = 12

g) 6 · [5 − 2 · (8 −13)] − 5 · [9 − 3 · (6 − 10)] = -15

h) (2 − 5) · [4 − 3 · (4 − 9)] − ( 2 − 7) · [15 − 2 · (9 − 4)] = -32

Ternas de pitagóricas

Una terna pitagórica consiste en una tupla de tres enteros positivos a, b, c que cumplen que a² + b² = c². El nombre deriva del teorema de Pitágoras, el cual plantea que en cualquier triángulo rectángulo, se cumple que x² + y² = z² (siendo x e y las longitudes enteras de sus catetos y z la de la hipotenusa).

Si m > n son enteros positivos, entonces:

a = m² − n²

b = 2mn

c = m² + n²

Las ternas pitagóricas suelen representarse como (a,b,c). Las ternas cuyos tres números son coprimos reciben el nombre de ternas pitagóricas primitivas. Las 16 primeras ternas pitagóricas primitivas, con c ≤ 100 son:

( 3 , 4 , 5 )	( 5, 12, 13)	( 7, 24, 25)	( 8, 15, 17)
( 9, 40, 41)	(11, 60, 61)	(12, 35, 37)	(13, 84, 85)
(16, 63, 65)	(20, 21, 29)	(28, 45, 53)	(33, 56, 65)
(36, 77, 85)	(39, 80, 89)	(48, 55, 73)	(65, 72, 97)

 Explicación en clase  


m > n

m	n	m2+ n2	M2 – n2	2mn
2	1	5	3	4
3	1	10	8	6
3	2	13	5	12
4	2	20	12	16
4	3	25	7	24

Cómo poner páginas en tu blog

-Para poner páginas en vuestro blog, tenéis que crear una entrada de prueba.
-A esa entrada de prueba, tenéis que ponerle todas las etiquetas del nombre que queráis llamar las páginas,por ejemplo;
Si quiero poner de páginas: Matemáticas,Lengua,Sociales,Comida,Juegos...Tendré que crear una entrada de prueba,y a esa entrada ponerle todas esas etiquetas.
-Después de crear la entrada,la publicáis en vuestro blog, luego entráis a esa entrada de prueba y hacéis clic en una de las etiquetas.
-Después de hacer clic en una etiqueta,copiáis la dirección de esa página(el https://... que aparece arriba).
-Luego vais a la entrada de blogger y os vais a diseño.En diseño buscais la palabra multicolumnas.
-Cuando hayáis encontrado multicolumnas le dais a añadir gadget,y buscais páginas y le haceis clic.
-Luego dais a añadir enlace externo y ponéis de título el de la pestaña que queréis crear,por ejemplo: Lengua.Luego pegáis la dirección que hemos copiado antes,CUIDADO,cuando copiáis la dirección tenéis que borrar un https// porque ya viene escrito.
-Dais a guardar y ya estaría vuestra página creada.
-Si queréis crear más pestañas,hacéis lo mismo, pero en diseño,en multicolumnas, ya no os pondrá añadir un gadget,tendréis que dar a editar y hay ya hacéis lo de antes.
-Cuando ya hayáis creado todas las páginas, podéis borrar la entrada de prueba.
-Si no os aparece la opción multicolumnas, tendréis que buscar otro tema en el que sí lo ponga.

HOLA

Ternas pitagóricas

Una terna pitagórica consiste en una tupla de tres enteros positivos a, b, c que cumplen que a² + b² = c². El nombre deriva del teorema de Pitágoras, el cual plantea que en cualquier triángulo rectángulo, se cumple que x² + y² = z² (siendo x e y las longitudes enteras de sus catetos y z la de la hipotenusa).

Primos de Mersenne

son de la forma 2n - 1 ntn 

n= 1:1 no es primo
n= 2:3 primo
n= 3:7"
n= 4:15=35 no es primo
n= 5:31 primo
n= 6:63 es múltiplo de 3. no es primo
n= 7:127 primo
n= 8:255 no es primo
n= 9:511 es múltiplo de 7, no es primo
n= 10:1023 ""3""
n= 11:2047 ""23"" no es primo
n= 12:4095 no es primo
n= 13:8191 primo


    

100 factorial

2(lo añadimos al final)

4 = 2 * 2                      2

6 = 2 * 3                      3

8 = 2 * 2 * 2                  6

9 = 3 * 3

10 = 2 * 5                     7

12 = 2 * 2 * 3                 9

14 = 2 * 7                     10

15 = 3 * 5

16 = 2 * 2 * 2 * 2             14

18 = 2 * 3 * 3                 15

20 = 2 * 2 * 5                 17

21 = 3 * 7

22 = 2 * 11                    18

24 = 2 * 2 * 2 * 3             21

25 = 5 * 5

26 = 2 * 13                    22

27 = 3 * 3 * 3

28 = 2 * 2 * 7                 24

30 = 2 * 3 * 5                 25

32 = 2 * 2 * 2 * 2 * 2 30

33 = 3 * 11

34 = 2 * 17                    31

35 = 5 * 7

36 = 2 * 2 * 3 * 3             33

38 = 2 * 19                    34

39 = 3 * 13

40 = 2 * 2 * 2 * 5             37

42 = 2 * 3 * 7                 38

44 = 2 * 2 * 11        40

45 = 3 * 3 * 5

46 = 2 * 23                    41

48 = 2 * 2 * 2 * 2 * 3 45

49 = 7 * 7

50 = 2 * 5 * 5                 46

51 = 3 * 17

52 = 2 * 2 * 13        48

54 = 2 * 3 * 3 * 3             49

55 = 5 * 11

56 = 2 * 2 * 2 * 7             52

57 = 3 * 19

58 = 2 * 29                    53

60 = 2 * 2 * 3 * 5             55

62 = 2 * 31                    56

63 = 3 * 3 * 7

64 = 2 * 2 * 2 * 2 * 2 * 2     62

65 = 5 * 13

66 = 2 * 3 * 11        63

68 = 2 * 2 * 17        65

69 = 3 * 23

70 = 2 * 5 * 7                 66

72 = 2 * 2 * 2 * 3 * 3 69

74 = 2 * 37                    70

75 = 3 * 5 * 5

76 = 2 * 2 * 19        72

77 = 7 * 11

78 = 2 * 3 * 13        73

80 = 2 * 2 * 2 * 2 * 5 77

81 = 3 * 3 * 3 * 3

82 = 2 * 41                    78

84 = 2 * 2 * 3 * 7             80

85 = 5 * 17

86 = 2 * 43                    81

87 = 3 * 29

88 = 2 * 2 * 2 * 11            84

90 = 2 * 3 * 3 * 5             85

91 = 7 * 13

92 = 2 * 2 * 23        87

93 = 3 * 31

94 = 2 * 47                    88

95 = 5 * 19

96 = 2 * 2 * 2 * 2 * 2 * 3     93

98 = 2 * 7 * 7                 94

99 = 3 * 3 * 11

100 = 2 * 2 * 5 * 5            96 + 1 = 97

100! = 2⁹⁷ · …

Por qué me enamoré de los números primos masivos

Definición     

Son millones de dígitos de longitud, y hace falta un ejército de matemáticos y computadoras para encontrarlos ¿No es para amar los números primos masivos? Adam Spencer el era apasionado de las matemáticas, comparte su pasión por estos extraños números y por la misteriosa magia de las matemáticas.

la definición más común de número primo era “un número que es divisible por 1 y sí mismo” 1 se ajusta a esta definición pero algunos matemáticos estaban preocupados por las formas en que uno es diferente de los otros números primos.


                             Lo que me aporta y entiendo 

demostró muchos hechos importantes básicos acerca de números primos que hoy damos por sentado como que hay infinitos números primos.

FACTORIAL DE UN NÚMERO NATURAL

FACTORIAL DE UN NÚMERO NATURAL 

El factorial de un entero positivo n, el factorial de n o n factorial se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n. Por ejemplo,

${\displaystyle 5!=1\times 2\times 3\times 4\times 5=120.\ }$

FACTORIAL DE UN NUMERO NATURAL

El factorial de un número natural se escribe como n! y se calcula multiplicando todos los números naturales inferiores a él.

6!-6·5·4·3·2·1=720

5!-5·4·3·2·1=120

4!-4·3·2·1=24